Disclaimer: MKLDNN Int8 primitives are a work in progress and not all definitions and configurations have been implemented or included in the documentation. Moreover, the example included in this documentation relies on int8 primitives which use the MKL binary dependency and is limited to MKLDNN built with the MKL binary.
Introduction
To push higher performance during inference computations, recent work has focused on computing at a lower precision (i.e. shrinking the size of data for activations and weights) to achieve higher throughput. Eight-bit computations (referred to as int8) offer improved performance over higher precision types -because it allows packing more data into a single instruction, at the cost of reduced but acceptable accuracy.
Int8 Workflow
Quantization Process
To operate with int8 data types from a higher precision format (e.g. 32-bit floating point), data must first be quantized. The quantization process converts a given input into a lower-precision format. The precision and accuracy factors are determined by the scale and rounding-mode respectively.
Scale
The scale is usually obtained from sampling the dataset of previous executions in the original format (e.g. the activations and weights from training in fp32) and is formulated as:
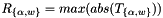
where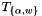 is a tensor corresponding to either the weights
is a tensor corresponding to either the weights 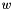 or the activations
or the activations 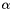 .
.
The purpose is to establish the range of values used in the computation where selecting a proper scaling factor prevents over or underflows when computing the lower precision results.
Quantization Factor
The next step is to calculate the quantization factor for converting the values into the corresponding int8 range. This is also known as the scale or scaling factor applied to the original high-precision values and is calculated as:
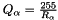 is the quantization factor for activations with non-negative values.
is the quantization factor for activations with non-negative values.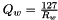 is the quantization factor for weights.
is the quantization factor for weights.
The low-precision values, known as the quantized activation, weights, and bias values are calculated as:
![$\alpha_{u8} = \lceil Q_{\alpha} \alpha_{f32} \rceil \in [0,255]$](form_29.png)
![$W_{s8} = \lceil Q_{w} W_{f32} \rceil \in [-127,127]$](form_30.png)
![$b_{s32} = \lceil Q_{\alpha} Q_{w} b_{f32} \rceil \in [-2^{31},2^{31}-1]$](form_31.png)
where the function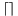 rounds to the selected rounding mode.
rounds to the selected rounding mode.
When the destination value (e.g. from a convolution) is stored as a signed 32-bit integer, the result is bound to the same quantization scaling factors:
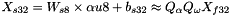
- where
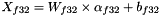
Where the approximated value is due to the rounded values.
Inversely, the dequantized value is calculated as:
Quantization Example
To show how the int8 parameters are obtained, suppose we first start off with a set of arbitrary high-precision input and output values. These values come from sampling a previously executed training run and are in their original 32-bit floating point format as:
- activations:
![$ T_{\alpha} = [15, 14, 15 ... 8, 11 ]$](form_36.png) where
where 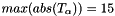
- weights:
![$ T_{\omega} = [-5.1 , 6.8, ... -1.2, 9.8 ]$](form_38.png) where
where 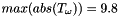
- bias:
![$ T_{\alpha} = [ 2.4, -5.2 ... -8 ]$](form_40.png) where
where 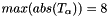
The scaling factors are:
Finally, the quantized input values for the 8-bit operation are calculated as:
These arrays are the new inputs for the int8 net.
MKLDNN Support for low-precision int8 Primitives
MKLDNN supports low-precision computations for inference through the int8 primitives. Int8 primitives are ordinary MKLDNN primitives which have their input and output parameters configured to 8-bit types. Int8 primitives are optimized for high performance, one example is the use of specialized 512-bit wide low-precision instructions available through the Advanced Vector Extensions 512 (AVX512) for Intel Skylake Server Systems. Currently, the 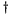 supported primitives are:
supported primitives are:
- convolution
- pooling
- eltwise
- sum
- concat
- reorder
MKLDNN Attributes
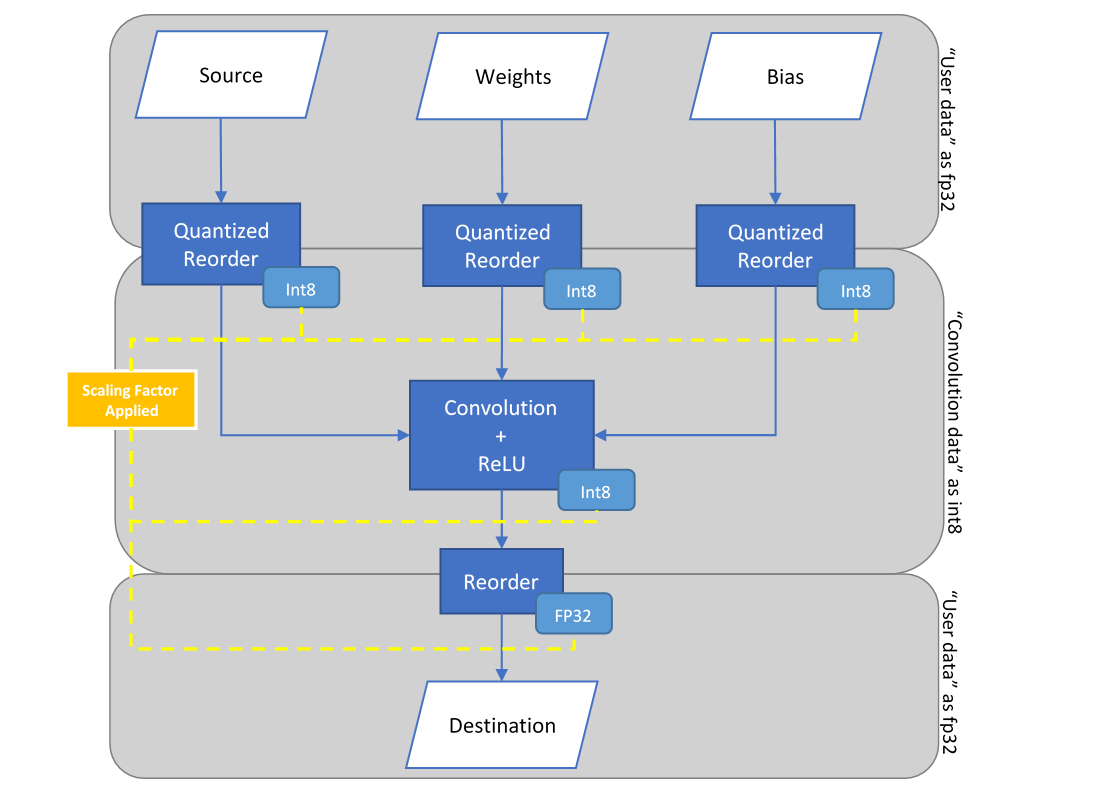
MKLDNN primitive behaviour may be extended for additional functionalities involving output data transformation. These additional features are configured via primitive attributes. The primitive attributes definition is an opaque structure for passing extra parameters to a primitive descriptor. These parameters include Scaling Factor, Round Mode and Fused Post-Operations (PostOps). All operation primitives support the attributes structure, however, not all configurations are implemented and result in failed primitive creation.
The scaling factor, as previously described, is known prior to the inference operation where the values are calculated from a set of formulas. In MKLDNN, the scaling factor is applied to the output of a primitive. Moreover, to perform input transformations (e.g. source, bias and weights), MKLDNN performs quantizing and dequantizing of data for int8 through the Reorder Primitive.
MKLDNN has 2 formats for defining the output scaling factor, depending on the configuration set by the scaling mask, the output is either scaled uniformly across all the dimensions (mask = 0) or a set of scaling values are applied to specific dimension(s), as explanation below:
- A single float-value shared across the tensor.
 Single-value scaling format
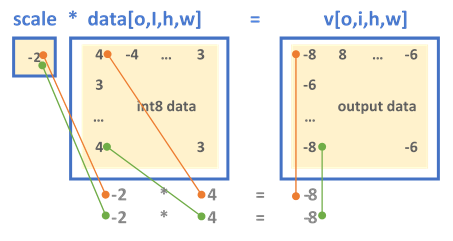
Single-value scaling format - An array of float values each corresponding to a specific output channel. The mask parameter determines the dimension to which the scales array is applied to where the ith-bit(s) of mask selects the dimension(s) di (where d is an n-dimensional output tensor with logical dimensions as [d0, d1, ..., dn-1]), for example:
 Multi-value scaling format
Multi-value scaling format - The single-scale format always has mask = 0.
- For a 5-dimensional tensor T[g0, o1,i2,h3,w4] where the numbering indicates the bit-index:
- A mask = 2 = 21 selects the output channel for scaling.
- A mask = 3 = 20 | 21 selects the group and output channels.
Note: Mask is always applied to the logical dimension; this is independent of the dimension format that the primitive might select. The dimensions in MKLDNN are defined as follows:
- 2D dimensional data the order of dimensions is always: (n, c)
- 4D dimensional data the order is always: (n, c, h, w)
- 5D dimensional weights the order is always: (g, oc, ic, kh, kw)
The Round Mode in attributes specifies the form of rounding for the resulting output value. Round mode will be applied whenever the output data type is not 32-bit floating point. The two options are:
- Nearest even integer value (default and recommended)
- Down (or floor) to the previous largest integer value.
Fused Post-Operations (PostOps) allow chaining operations during the primitive computation. Note that the resulting output value from PostOps is always affected by the scaling factor. The supported operations are:
- Accumulation where the primitive sums the resulting values from previously computed activations as:
![$ dst[ ] \leftarrow scale * dst[] + op(...); instead of dst[ ] \leftarrow op(...) $](form_48.png)
- Element-wise (eltwise) operation with kind, alpha and beta parameters as:
![$ dst[ ] \leftarrow scale * eltwise_op ( op(...) ); instead of dst[ ] \leftarrow op(...)$](form_49.png)
The list of supported eltwise operations for int8 is currently limited to ReLU. For instance, PostOps may only configure a convolution with accumulation followed by eltwise (relu).
Simple_Net.cpp Example using 8-bit and PostOps Computations
The MKLDNN repository contains an example called simple_int8_net.cpp that executes a Convolution with ReLU from the AlexNet topology using int8 computations. This example extends the simple_net.cpp source focusing on the creation and execution of int8 primitives using PostOps and Scaling Factors to obtain similar results.
- Initially, the example configures the tensors according to the dimensions in Conv3 of AlexNet. memory::dims conv_src_tz = { batch, 256, 13, 13 };memory::dims conv_weights_tz = { 384, 256, 3, 3 };memory::dims conv_bias_tz = { 384 };memory::dims conv_dst_tz = { batch, 384, 13, 13 };memory::dims conv_strides = { 1, 1 };auto conv_padding = { 1, 1 };
- Next, the example configures the scales used to quantize fp32 data into int8. For this example, the scaling value is chosen as an arbitrary number, although in a realistic scenario, it should be calculated from a set of precomputed values as previously mentioned. The source, weights, bias and destination datasets use the single-scale format with mask set to ‘0’, while the output from the convolution (conv_scales) will use the array format where mask = 2 corresponding to the output dimension./* Set Scaling mode for int8 quantizing */const std::vector<float> src_scales = { 1.8 };const std::vector<float> weight_scales = { 2 };const std::vector<float> bias_scales = { 1 };const std::vector<float> dst_scales = { 0.55 };/* assign halves of vector with arbitrary values */std::vector<float> conv_scales(384);const int scales_half = 384 / 2;std::fill(conv_scales.begin(), conv_scales.begin() + scales_half, 0.3);std::fill(conv_scales.begin() + scales_half + 1, conv_scales.end(), 0.8);const int src_mask = 0;const int weight_mask = 0;const int bias_mask = 0;const int dst_mask = 0;const int conv_mask = 2; // 1 << output_channel_dim
- Create the memory primitives for user data (source, weights and bias). The user data will be in its original 32-bit floating point format. auto user_src_memory = memory({ { { conv_src_tz }, memory::data_type::f32, memory::format::nchw },cpu_engine },user_src.data());/* ... */
Create a memory descriptor for each convolution parameter. The convolution data uses 8-bit integer values, so the memory descriptors are configured as:
- 8-bit unsigned (u8) for source and destination.
- 8-bit signed (s8) for bias and weights.
Note: the destination type is chosen as unsigned because the convolution applies a ReLU operation where data results ≥ 0.
auto conv_src_md = memory::desc({ conv_src_tz }, memory::data_type::u8, memory::format::any);/* ... */auto conv_dst_md = memory::desc({ conv_dst_tz }, memory::data_type::u8, memory::format::any);- Create a convolution descriptor passing the int8 memory descriptors as parameters. auto conv_desc = convolution_forward::desc(prop_kind::forward,convolution_direct, conv_src_md, conv_weights_md, conv_bias_md,conv_dst_md, conv_strides, conv_padding, conv_padding,
Configuring int8-specific parameters in an int8 primitive is done via the Attributes Primitive. Create an attributes object for the convolution and configure it accordingly.
primitive_attr conv_attr;/* Specify the rounding mode */conv_attr.set_int_output_round_mode(round_mode::round_nearest);/* Specify the scales array and corresponding mask */conv_attr.set_output_scales(conv_mask, conv_scales);The ReLU layer from Alexnet is executed through the PostOps feature. Create a PostOps object and configure it to execute an eltwise relu operation.
const float ops_scale = 1.;const float negative_slope = 0.;post_ops ops;ops.append_eltwise(ops_scale, algorithm::eltwise_relu, negative_slope, 0.);conv_attr.set_post_ops(ops);- Create a primitive descriptor using the convolution descriptor and passing along the int8 attributes in the constructor. The primitive descriptor for the convolution will contain the specific memory formats for the computation. auto conv_prim_desc = convolution_forward::primitive_desc(conv_desc, conv_attr, cpu_engine);
- Create a memory primitive for each of the convolution’s data input parameters (source, bias, weights and destination). Using the convolution primitive descriptor as the creation parameter allows MKLDNN to configure the memory formats for the convolution. Scaling parameters are passed to the reorder primitive via the attributes primitive.auto conv_src_memory = memory(conv_prim_desc.src_primitive_desc());primitive_attr src_attr;src_attr.set_int_output_round_mode(round_mode::round_nearest);src_attr.set_output_scales(src_mask, src_scales);
- User memory must be transformed into convolution-friendly memory (for int8 and memory format). A reorder layer performs the data transformation from fp32 (the original user data) into int8 format (the data used for the convolution). In addition, the reorder will transform the user data into the required memory format (as explained in the simple_net example). auto src_reorder_pd= reorder::primitive_desc(user_src_memory.get_primitive_desc(),conv_src_memory.get_primitive_desc(), src_attr);net.push_back(reorder(src_reorder_pd, user_src_memory, conv_src_memory));/* ... */
- Create the convolution primitive and add it to the net. The int8 example computes the same Convolution +ReLU layers from AlexNet simple-net.cpp using the int8 and PostOps approach. Although performance is not measured here, if it were, in practice, it would require less computation time to achieve similar results. net.push_back(convolution_forward(conv_prim_desc, conv_src_memory,conv_weights_memory, conv_bias_memory, conv_dst_memory));
- Finally, dst memory may be dequantized from int8 into the original fp32 format. Create a memory primitive for the user data in the original 32-bit floating point format and apply a reorder to transform the computation output data. auto user_dst_memory = memory({ { { conv_dst_tz }, memory::data_type::f32, memory::format::nchw },cpu_engine },user_dst.data());primitive_attr dst_attr;dst_attr.set_int_output_round_mode(round_mode::round_nearest);dst_attr.set_output_scales(dst_mask, dst_scales);auto dst_reorder_pd= reorder::primitive_desc(conv_dst_memory.get_primitive_desc(),user_dst_memory.get_primitive_desc(), dst_attr);
The diagram to summarize this example is as follows:
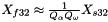
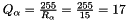
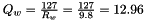
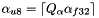
![$ = \lceil 17 \times [15, 14, ... 11 ] \rceil = [255, 238, ... 187] $](form_45.png)
![$W_{s8} = \lceil Q_{w} W_{f32} \rceil = \lceil 12.96 \times [-5.1 , 6.8, ... -1.2, 9.8 ] \rceil = [-66, 88, ... -15, 127] $](form_46.png)
![$b_{s32} = \lceil Q_{\alpha} Q_{w} b_{f32} \rceil = \lceil 17 \times 12.96 \times [ 2.4, -5.2 ... -8 ] \rceil = [528, -1145, ... -1762] $](form_47.png)
 1.8.13
1.8.13